支持向量机(SVM)

支持向量机是一种用于分类的算法。如果数据是线性可分的，只需要将直线放置在让点距离平面距离最大的位置，寻找这个最大间隔的过程叫做最优化；如果数据不是线性可分的，需要用核函数改变维度，用超平面做分类……

线性SVM

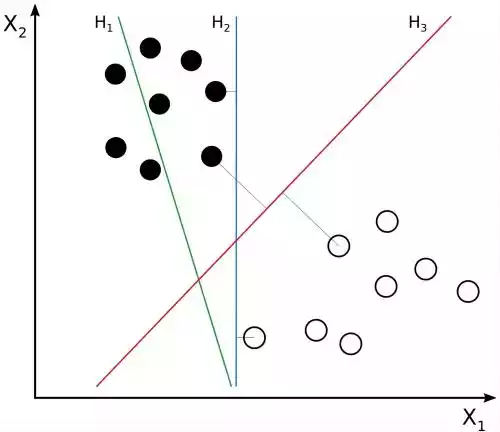
如图，数据显然是线性可分的，这些将它们分类的直线称为决策面，每个决策面对应一个线性分类器。但是将它们分开的直线显然不止一条。目前和的分类效果相同，但如果再增加一个点（在和​之间），就会出现分类错误。

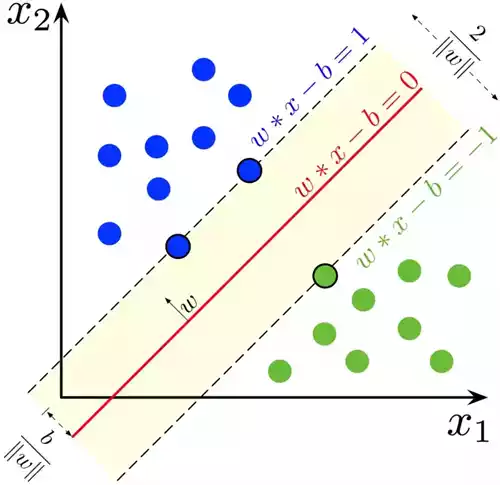
图中虚线的位置由决策面的方向和距离决策面最近的几个样本位置决定，虚线穿过的样本点称为支持向量，中间的部分是分类间隔。具有最大间隔的决策面就是SVM要找的最优解。

数学建模

  • 目标函数：希望使得什么指标最好，即分类间隔
  • 优化对象：可以改变的影响因素，即决策面

优化对象（决策面）

在二维空间中，一条直线可以表示为 设其中，，是这条直线的法向量，是截距。把二维平面的直线推广到维空间，就得到了超平面方程 此时的，​。

目标函数（分类间隔）

分类间隔的大小是支持向量的样本点到决策面距离的二倍，二维平面中，点到直线的距离公式是 推广到多维 分类间隔​越大，表示对应的超平面分类效果越好。

约束条件

  • 判断决策面将样本点正确分类
  • 选出支持向量上的点

图中有两类点，分别对它们做标记，蓝色的标记为，规定为正样本；绿色的标记为，规定为负样本。 如果超平面能对上图样本点正确分类，则有 再提高一点要求，决策面处于分类间隔的中间，则 所有标签为的样本到决策面的距离都大于等于，标签为的点到决策面的距离都小于等于.

两边同除，得到 其中，​，综合两个式子可以得到一个约束条件 并且，支持向量满足，则目标函数可以简化为 于是最大化的问题转化为最小化的问题。

最终最优化问题的建模为

最优化问题

Lagrange乘数法

Lagrange乘数法

  • 等式约束优化问题

令，函数称为函数，为乘子 其中和均为优化变量。

  • 不等式约束优化问题

上一部分得出的优化问题的约束条件是一个不等式，现在需要引入松弛变量，将其转化为等式约束条件，同时松弛变量也是一个优化变量。

原优化问题 设，​，引入松弛变量，得到新的等式约束条件为

并得到函数为 联立必要条件的方程得 当时，，则，；当时，，则方程组转化为 即不等式约束优化问题的KKT条件。

目标，即 $$

其中，则目标可以转化为 L(, ) = f() + _{i=1}^n _i g_i() $$ 其中，假设，，现在要找到最优的，使得接近，则问题转化为.

此时最优化问题转化为

对偶性

，有.

最大的里面挑出个最小的比最小的里面的最大的大~

当等号成立时满足强对偶关系，是凸优化问题

SVM最优化流程

目标函数与约束条件： 强对偶性转化： 对参数求偏导 得到 代入到目标函数 此时最优化问题为

SMO算法

由，选择和，设，其中，由此得出

此时，相当于将问题转化为只有一个约束条件的最优化问题，之后利用Lagrange乘数法求最优解即可。

再由可以求得，所有即的点都是支持向量，找到后带入即可求得，最后就能构造出超平面 分类决策函数为

对于验证集的点，带入决策函数即可得到其分类。

未完待续……

参考资料

  1. Support vector machine(Wikipeda)
  2. KKT条件，原来如此简单 | 理论+算例实践
  3. Python3《机器学习实战》学习笔记（八）：支持向量机原理篇之手撕线性SVM
  4. Python3《机器学习实战》学习笔记（九）：支持向量机实战篇之再撕非线性SVM
  5. 【机器学习】支持向量机 SVM（非常详细）