信息论基础
信息论基础
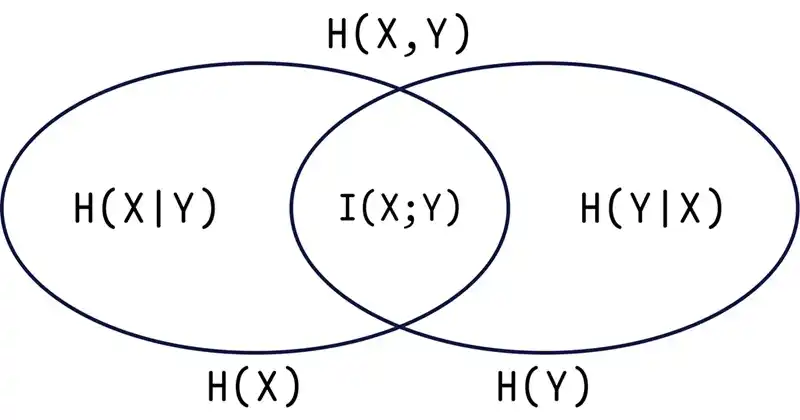
熵和互信息的关系
相对熵(KL距离)
相对熵衡量的是同一事件空间中两个概率分布的差异,不是距离。
在同一事件空间中,概率分布
对应的每个事件如果用 编码,平均每个基本事件编码长度增加了多少比特。
用
- 非负性(由吉布斯不等式可证)
若
,则 ,当且仅当 时取等
- 不满足对称性(交叉熵
相对熵) - 不满足三角不等式
数据处理不等式
如果
记为
数据越传损失的越多;数据
的函数不会增加关于 的信息量~
如果
通过观察
, 与 的依赖会降低~
Fano不等式
(+﹏+)~晕,待续……
渐进均分性
收敛
- 收敛:图像逐渐趋近于某条横线
- 几乎确定收敛:图像逐渐趋近于某条横线,但是有几个点各色
- 依概率收敛:
大数定理
- 强大数定理:
一直向 靠近
- 弱大数定理:
向 靠近的可能性越来越大
渐进均分定理(AEP)
当序列足够长,其中一部分序列就会显示出某种固定的性质,即各个符号出现的频率接近于概率,而这些序列的的概率则趋近于相等,且它们的和非常接近于
数学定义为:若
典型集
若
性质
- 若
,则 ,典型集中的元素个数 - 当
时, - 当
,
数据压缩
数据压缩时把一个完整的概率空间缩小到典型集,而典型集相对整个空间来说时非常小的,且高概率出现,这就起到了压缩的作用。
典型集的个数很少
如果全空间有
个元素,根据性质2它大概有 个元素。
这说明典型集的个数相对于全空间来说时很小的,但他确实高频率出现的。
数据压缩
- 将集合元素按照某种顺序排列;
- 指定下标可表示
中的每个序列; 需要 比特; - 编码加
,则编码 需要 比特; - 同理,对于非典型集
需要 比特,编码加 需要 比特; - 获得一个
一个编码方案;
其中非典型集的比特数是用全空间序列计算的,因为典型集个数很少,可以用全空间元素个数代替非典型集元素个数,误差可以忽略。
编码方案
设
熵率
前文中的渐进均分性(AEP)表示平均意义下使用
马尔科夫链
用马尔科夫链可以减少研究随机过程问题的维度。
马尔科夫过程的每一步结果最多只与上一步有关,与其它步骤无关,数学表示为
马尔科夫链不是一个真正与历史无关的过程,通过链式法则,历史的信息可以传递到现在。
信道容量
香农信道容量公式
- 在信道中当传输系统的
下降时,可以用增加系统传输带宽 的办法来保持信道容量 不变; - 在高斯白噪声干扰情况下,在平均功率受限的信道上,实现有效和可靠通信的最佳信号是具有白噪声统计特性的信号。