从复数到四元数
复数与二维旋转
设复数 ,则 将这个结果写成矩阵相乘的形式, 说明 矩阵 表示的几何变换与是复数乘法运算等价的。
一般地,向量 在二维平面中对应一个直角三角形,两个直角边长度为 和 ,斜边长为 ,即向量的模长,矩阵 的每个元素同时除以模长,得到 设向量 与 轴夹角为 ,则 . 与该矩阵相乘在二维平面上实现的效果是 被乘的向量绕原点逆时针旋转 .
由此可以发现,复数能够表示二维平面上的旋转,假设旋转角度为 ,定义单位复数旋转因子为 被旋转的向量 ,相乘得到被旋转 后的复数为 对应向量 在二维平面 中绕原点逆时针旋转了 .
四元数与三维旋转
本文仅使用右手坐标系。
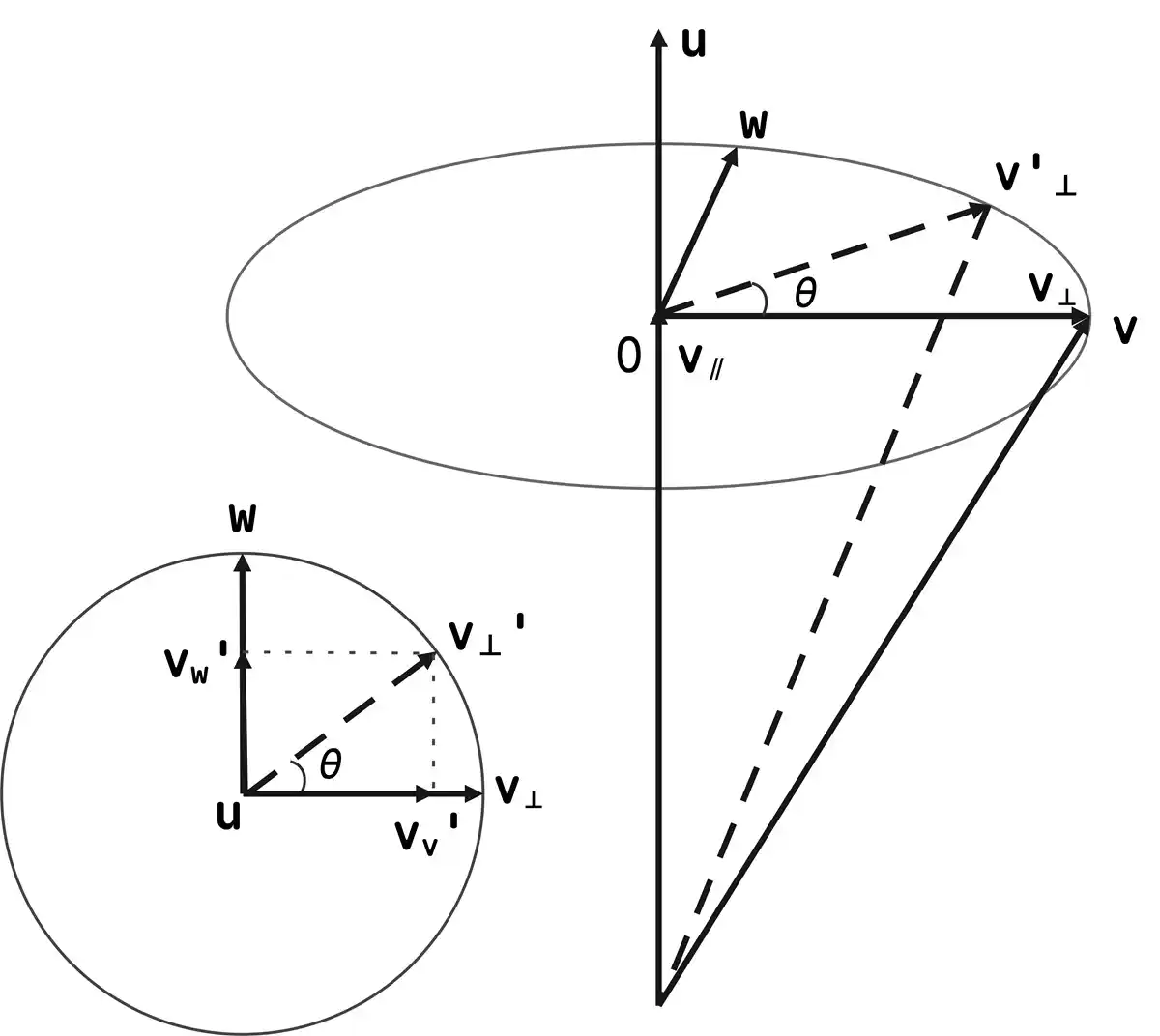
在三维空间中,向量 绕某个旋转轴 旋转,可以将向量 分解为平行于 的分量 和垂直于 的分量 ,然后分别旋转这两个向量,再合并得到最后结果。
其中 始终与 重合,旋转 后的 ;
始终与 垂直,它的旋转可以看作二维平面内的旋转,如下图所示,
 向量 绕旋转轴 , 旋转的结果
向量 绕旋转轴 , 旋转的结果
为了用“复数”形式表示类似的旋转,最简单的想法是在复数域再加一个维度,即在复数的基础上增加一个虚数 ,假设三维空间中的“复数”为 显然, 与 相乘得到的结果中包含 这些交叉乘积项,并没有已知定义(与 不在同一个向量空间中),因此不能表示三维空间中旋转的结果。
在二维平面中,向量可以在 平面旋转,只需要一个虚数,而在三维空间中,向量旋转等效于在 三个平面旋转,或许需要三个虚数表示才可以。
于是定义四元数,表示为 , 其中 表示三个维度,并且根据笛卡尔坐标系下的外积运算法则,定义 
金雀花桥上的纪念石刻(图片来源于网络)
定义两个四元数 令 ,相乘并化简得到 其中 其余部分将 提出,得到 最后得到两个四元数相乘的结果为 也可以将相乘结果写成 该乘法结果可以表示成矩阵形式 与矩阵类似,四元数的乘法并不遵循交换律。类比矩阵的逆的定义,定义四元数乘法的逆运算为 ,满足 与复数的共轭类似,定义四元数 的共轭为 满足 则有 并且对于单位四元数来说,.
回到最初讨论的三维空间中的旋转问题,令 , 表示三维空间的向量,相乘结果为 为了使得旋转后的结果仍为三维向量,需要满足 ,即 .
只有虚部的四元数称为纯四元数,表示为 ,两个纯四元数的乘积为
基于前文向量 绕旋转轴 的讨论,将向量均用纯四元数表示
向量 旋转后的结果
向量 旋转后的结果 已知 ,则 由此可以得出,完成旋转 这一变换的单位四元数可以构造为 单位向量 指向转轴方向,待转向量 正交于 时,将旋转变换用四元数形式改写为
一般地,
令 ,则 最终得出结论,任意向量 绕指向转轴方向的单位向量 旋转 ,旋转后的 可以用下面运算得到 其中 .
在表示二维平面中的旋转时,利用欧拉公式可以将旋转表示为指数形式 ,类似地,对于单位四元数 ,有 于是前面四元数的旋转表达式可以写成
考察四元数 的变换, 与 的变换相同。从几何角度考虑, 表示绕转轴旋转 ,而 表示绕相反的转轴旋转 ,所以说 单位四元数与三维旋转是一个二对一的满射同态关系。
四元数插值与三维旋转
前置知识:线性插值
已知函数 在两点的值,要获得其它点数值,
与函数的线性插值类似,下面讨论四元数的插值,用单位四元数 表示第一个方向, 表示第二个方向, 表示最终的方向。
与线性插值类似,当插值参数 时,插值的效果是将 旋转到 ,当 时,插值的效果是将 旋转到 。
旋转的对象是角度,从指数形式 考虑,“线性插值”的对象是四元数的指数,类比写出四元数插值的形式
其中 与 的角度差 ,即 当插值系数 时,,当时,。
注:四元数不止有一种定义形式,本文仅涉及 Hamilton 形式。
参考资料
张小飞, 李建峰, 徐大专, 等.阵列信号处理及 MATLAB 实现[M].电子工业出版社,2020.(2.3 四元数理论)
Krasjet/quaternion
从复数乘法到旋转矩阵 - YourMath