判圈法

Floyd判圈法

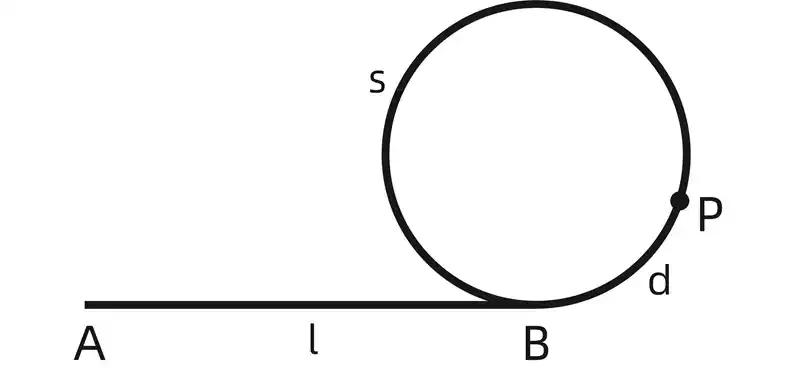
利用快慢指针，快指针步进速度为慢指针的两倍，若是链表中存在环，则两个指针一定会相遇，且快指针路程比慢指针路程多圈长度的整数倍。

假设两个指针在点相遇，则有

快指针：
慢指针：

class Solution {
public:
    static bool hasCycle(ListNode *head) {
        if (head == nullptr || head->next == nullptr) {
 			return false;
        }
        ListNode *low = head;
        ListNode *fast = head->next;
        while (fast != nullptr) {
            if (fast == low) {
            	return true;
            }
            if (fast->next == nullptr) {
                return false;
            }
            fast = fast->next->next;
            low = low->next;
        }

        return false;
    }
};

在验证存在环的前提下，令快指针不动，慢指针向后遍历节点，再次和快指针相等时，慢指针的步数即为环的长度。

在验证存在环的前提下，令慢指针回到起点，两个指针以相同速度步进，再次相遇时相遇点即为环起点。

上文已证明，则，进而得到，即所以当慢指针步进到达环起点时，快指针也从步进，距离环起点为环长度的整数倍，则快指针也到达了环起点。

Brent判圈法

令快慢指针指向起始节点，慢指针保持不动，快指针走步，快指针每走一步，判断快慢指针是否相遇，如果相遇则存在环，如果走了步后没有相遇或走到头，则将慢指针的位置移到快指针处，走下一轮……

第轮存在环的条件是，环长度；