卫星通信
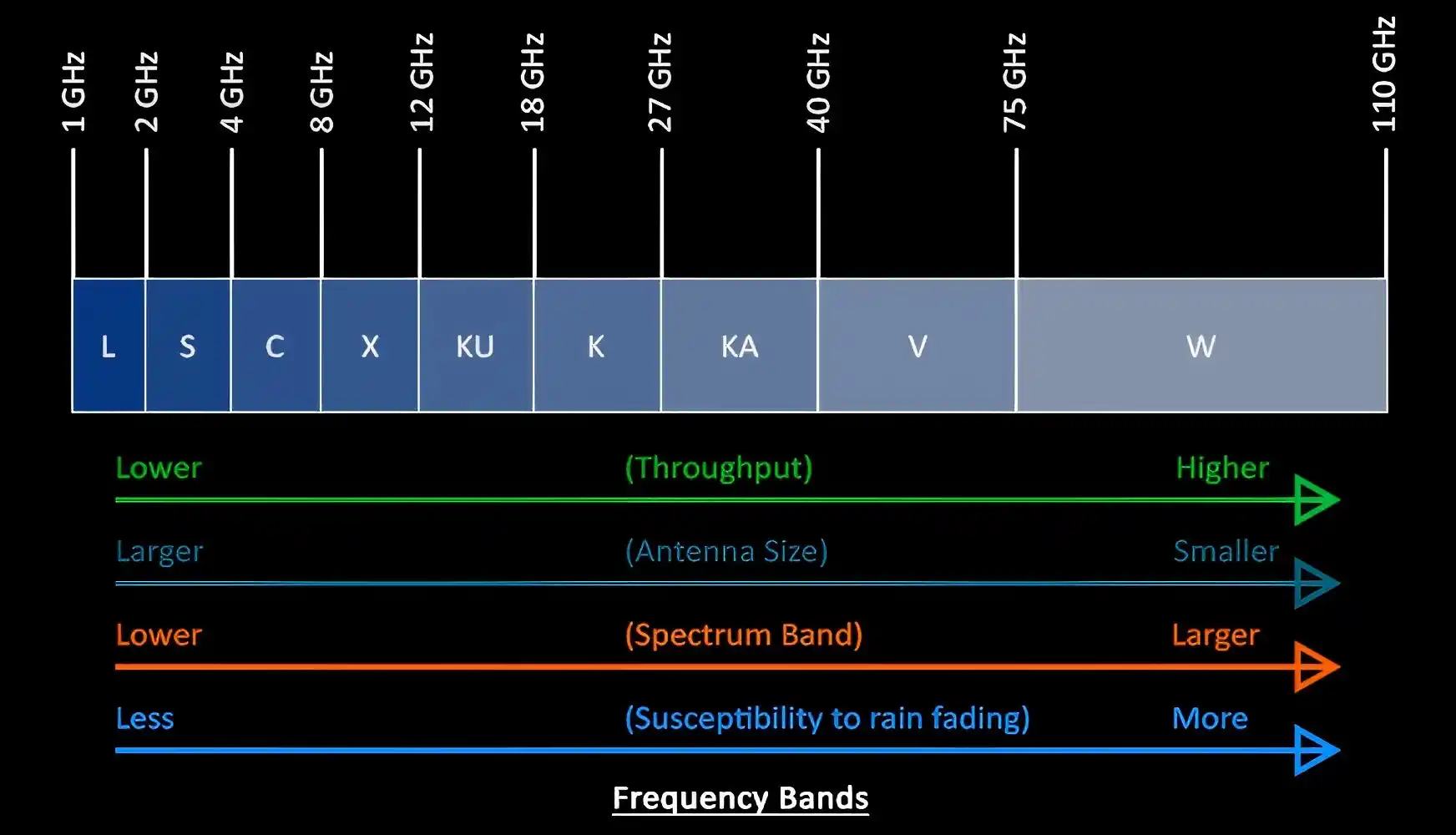
频段
航天器运行轨道
- 低地(球)轨道近地(球)轨道(LEO:Low Earth Orbit)
- 轨道高度:约400-2000公里;
-
应用:绝大多数对地观测卫星、测地卫星、空间站以及一些新的通信卫星系统。
-
中地球轨道(MEO:Middle Earth Orbit)
- 轨道高度:2000-36000公里之间;
-
应用:GPS、GLONASS等导航卫星系统。
-
地球同步转移轨道(GTO:Geostationary Transfer Orbit)(椭圆轨道)
- 特点:近地点在1000公里以下、远地点为地球同步轨道高度(约36000公里);
-
应用:为霍曼转移轨道的运用之一,经加速后可达地球静止轨道(GEO)。常以地球同步转移轨道酬载能力作为火箭性能指标。
-
地球同步轨道(GEO:Geostationary Orbit)
- 轨道高度:约36000 km;
- 特点:卫星运行方向与地球自转方向相同、运行轨道为位于地球赤道平面上圆形轨道、运行周期与地球自转一周的时间相等(23时56分4秒),卫星在轨道上的绕行速度约为3.1公里秒。
- 应用:布设3颗通讯卫星即可实现除两极外的全球通讯。
地球同步轨道分为以下三种:
-
地球静止轨道(GEO:Geostationary Orbit)(正圆轨道)
- 特点:轨道面的倾角为零度,卫星在地球赤道上空运行,从地球上仰望卫星仿佛悬挂在太空静止不动。
-
倾斜地球同步轨道(IGSO:Inclined Geosynchronous Orbit)
- 特点:倾角不为0的地球同步轨道,星下点轨迹是一个跨南北半球的“8”字。
-
极地轨道同步轨道,又叫太阳同步轨道(SSO:Sun-synchronous Orbit)
- 特点:卫星的轨道平面和太阳始终保持相对固定的取向,轨道倾角接近90度。适用于全球范围内进行观测和应用的气象卫星、导航卫星、地球资源卫星等。
- 应用:倾斜轨道和极地轨道同步卫星从地球上看是移动的,但每天可以经过特定的地区,用于科研、气象或军事情报的搜集,以及两极地区和高纬度地区的通信。
定位
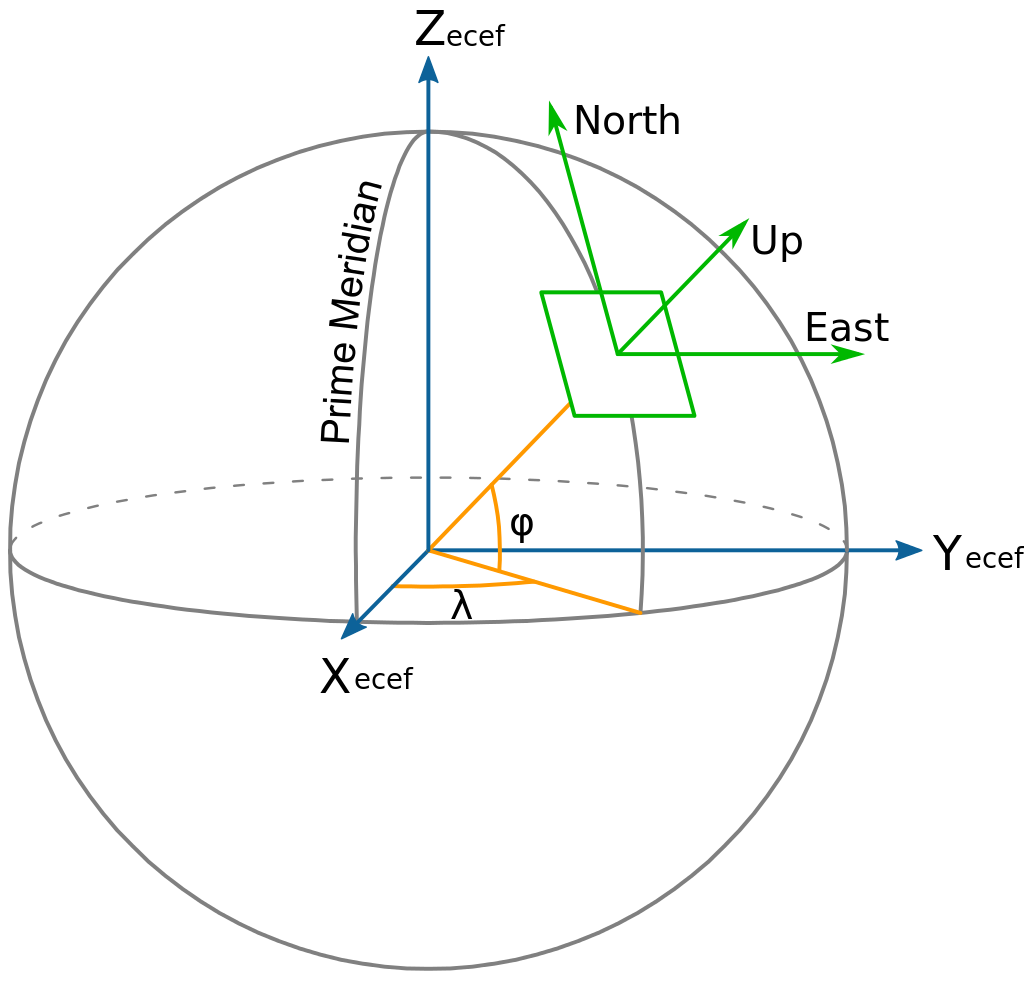
ECEF到ENU的旋转矩阵
ECEF(地心地固坐标系)到ENU(东北天站心坐标系)的转换需基于站心点的经纬度(记为纬度$ B \(、经度\) L $,单位为弧度),通过旋转变换实现。转换过程中需先将ECEF坐标平移至站心点,再通过旋转矩阵将地心坐标系转换为局部ENU坐标系。
ECEF到ENU的旋转矩阵由两次基本旋转组合而成,旋转顺序为:
- 绕Z轴旋转\(-(\dfrac{\pi}{2} + L)\)(修正经度方向);
- 绕X轴旋转\(-(\dfrac{\pi}{2} - B)\)(修正纬度方向);
根据正交矩阵性质及三角函数变换,推导得到最终旋转矩阵\(R\)如下:
$$
R = \begin{bmatrix}
-\sin L & \cos L & 0 \
-\sin B \cos L & -\sin B \sin L & \cos B \
\cos B \cos L & \cos B \sin L & \sin B \
\end{bmatrix}
$$
其中:
- $ L \(为站心点经度(弧度),\) B $为站心点纬度(弧度);
-
矩阵列向量分别对应ENU坐标系的东、北、天方向在ECEF坐标系中的单位向量;
-
东向(E):由经度$ L \(决定,对应矩阵第一行:\)[- \sin L, \cos L, 0]$;
- 北向(N):由纬度$ B \(和经度\) L \(共同决定,对应矩阵第二行:\)[- \sin B \cos L, -\sin B \sin L, \cos B]$;
- 天向(U):由纬度$ B \(决定,对应矩阵第三行:\)[\cos B \cos L, \cos B \sin L, \sin B]$;
设站心点ECEF坐标为\((X_p, Y_p, Z_p)\),目标点ECEF坐标为\((X, Y, Z)\),则ENU坐标\((e, n, u)\)的计算步骤为:
- 计算ECEF坐标增量:\(\Delta X = X - X_p,\ \Delta Y = Y - Y_p,\ \Delta Z = Z - Z_p\);
- 应用旋转矩阵: